
What is a Signed Distance Function?
and why should you care?
Signed Distance Functions allow you to generate graphics that can be applied to a surface in a game. Unlike textures, SDF masks can be resolution-independant, require almost zero memory, and can be parameterised to animate in ways that are simply impossible with textures alone. They are a powerful and essential tool in a technical artists toolbelt.
Let's clarify some of these terms:
Signed Distance Functions are functions that operate on a domain and return the distance to the surface of a shape.
The distance value that is returned is a Signed Distance Field, and this field can be sampled to generate several useful things, including but not limited to a shapes, surface properties, raymarched 3D renders, text glyphs and more.
Domain
The domain is the input of a signed distance function. It is a (usually continuous) space upon which signed distance functions operate. Domains can be 1D, 2D, 3D, or more, when needed.
In games, the most common 2D domain is UV Coordinates
The most common 3D domain is World Position
Vertex colour and Screen position are also fairly commonly used.
Field
A field is the output of a signed distance function.
In a continuous domain, a field can be thought of as a gradient where negative numbers indicate the distance inside a shape, a value of 0 indicates the surface of a shape, and positive numbers indicate the distance outside a shape.
Shape
A greyscale mask which can be used to render your result. A shape might be a n-dimensional primitive, such as a sphere, cube, torus, cone, star, or ngon.
Not all fields/shapes are generated procedurally, as we will look at in texture-based fields later.
Sampling
Sampling is the method by which we generate shapes from fields. Which sampling technique you use depends on how many dimensions you're working with, and how you intend to use the result.
2D Sampling usually uses smoothstep to generate a mask from a field mask.
3D Sampling usually uses raymarching to draw a 3D scene inside a 2D renderer. Raymarching is a relatively expensive operation and whilst it can be viable, it's less common in games.
A Simple Example
To demonstrate an example SDF application, let's look at a simple sdSphere operation.
Though simple, this exact method has been used countless times in ui elements, weapon pickups, achievement notifications, even on 2D animated characters.
Since the domain is in uv space, the units for radius and offset are "uv". A value of 0.5 for offset will give the result "half a uv tile".
// Psuedo Example
// Generate a 2D Distance Field for a 2D sphere (aka. a circle) of a given radius.
float sdSphere(float2 domain, float radius) {
return length(domain) - radius;
}
// Use smoothstep to sample our field between the surface of the field and just inside it.
// This is a "fixed" sampling method. Other methods use ddx/ddy to get "variable" smoothness depending on view angle/distance.
float sampleSmooth(float field, float smoothing) {
// I like to use -0.01 when sampling on uvs so that a smoothing value of 1 gives a nice result.
smoothstep(0., -0.01 * smoothing, field);
}
// Get the UV of the mesh (In this case, a quad).
float2 uv;
// Offset in x and y to "move" our domain. 0.5 will center the domain.
uv -= offset;// 2D Domain
// Run our distance function to get our field.
field = sdSphere(uv, radius); // 2D Field
// Sample our field to get a 2D mask.
return sampleSmooth(field, smoothing); // 2D Mask2D Domain
2D Field
2D Mask
Uniforms
Shader Parameters
Shader parameters can be passed in from your engine to dynamically change the results of your field.
Shader Graphs
Node based SDF
It is, of course, perfectly possible to translate almost all SDF techniques to material function/subgraph versions, for use in a shader graph.
By wrapping the field generation functions, field operations, and sampling operations into their own nodes, fields can be easily used even by artists who are less comfortable with maths.
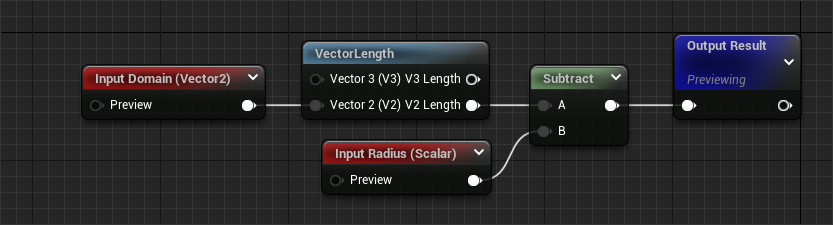
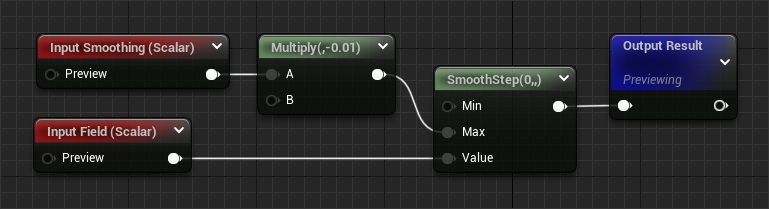
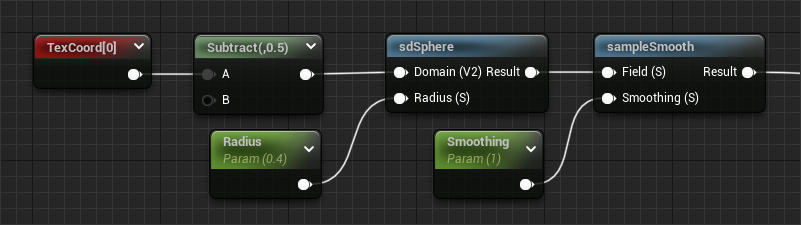
Visualized Field
Visualizing Fields
A Quick Trick
When trying to observe a field, all the negative values (distance values inside the shape) appear black, and it can be tricky to even see the exact edge of the shape.
From here, I'll run the field value through a visualise function - grey values will be outside the shape, and blue values will be inside the shape. This function also serves to demonstrate how easy it is to build beautiful and complex graphics from even simple fields.
float3 visualize(float d) {
// Start with solid blue inside and solid grey outside.
float3 col = (d>0.0) ? float3(0.25) : float3(0.054,0.450,.819);
// Have brightness falloff from the surface exponentially.
col *= 1.0 - exp(-6.0*abs(d));
// Use a fixed smoothstep sampling technique
// on a modified version of the field to draw concentric rings.
float m = smoothstep(0.35, 0.45, abs(frac(d * 25.) - 0.5));
col *= 0.8 + (0.2 * m);
// Draw a thin white line around the surface.
col = lerp( col, float3(1.0), 1.0-smoothstep(0.0,0.005,abs(d)) );
return col;
}Writing Distance Functions
Get started in Unreal & Unity
You can't write about SDF without mentioning the brilliant Inigo Quilez.
Most of the mathematics that I use when working with SDF comes from IQ.
Booleans
Unlike in polygon based 3D geometry, boolean operations with distance fields (When those fields are constructed properly) actually work.
By combining multiple fields in interesting ways, complex shapes can be built up that are useful far beyond simple primitives.
Union, Subtraction, and Intersection are the basic building blocks of boolean operations, but there are also special "smooth" boolean operations which give you a smoother transition at the cost of field integrity.
Smooth booleans can distort the field leading inconsistent field density - You can see this in the stretching of the lines in the demos below. This can be somewhat counteracted with this technique, or when your result is going to be a mask, dynamic sampling approaches (ddx/ddy) can also help.
It's worth noting that subtraction does not result in a accurate external distance field. In most cases, this isn't a problem.
float2 opUnion(float a, float b) {
return min(a,b);
}
float opSubtraction(float a, float b) {
return max(-b, a);
}
float opIntersect(float a, float b) {
return max(a, b);
}
float opExclusion(float a, float b) {
return opUnion(opSubtraction(a,b), opSubtraction(b,a));
}
float opSmoothUnion(float d1, float d2, float k) {
float h = clamp( 0.5 + 0.5*(d2-d1)/k, 0.0, 1.0 );
return mix( d2, d1, h ) - k*h*(1.0-h);
}
float opSmoothSubtraction(float d1, float d2, float k) {
float h = clamp( 0.5 - 0.5*(d2+d1)/k, 0.0, 1.0 );
return mix( d2, -d1, h ) + k*h*(1.0-h);
}
float opSmoothIntersection(float d1, float d2, float k) {
float h = clamp( 0.5 - 0.5*(d2-d1)/k, 0.0, 1.0 );
return mix( d2, d1, h ) + k*h*(1.0-h);
}Union
min(a,b)
Subtraction
max(-b, a)
Intersection
max(a,b)
Exclusion
min(max(-b,a), max(-a,b))
Smooth Union
Smooth Subtraction
Smooth Intersection
Uniforms
Shader Parameters
Adjust the boolean operators and smoothing k-value.
Rounding
Making a distance field rounded is simple and useful. By subtracting a radius value from the field, you can essentially offset the surface of the shape being represented, which implictly rounds corners.
Since we usually want to round corners without "inflating" the shape, I usually adjust the size parameter of the shape I'm working with to subtract the radius before passing the resulting field to the rounding function, in order to counteract the upcoming inflation.
It can sometimes also be a good idea to clamp the radius to avoid cases where the radius exceeds the size of the shape. Other times, unclamped values can give useful results.
// Consider using the r value in your initial distance function so your field compensates for the "inflation" this will manifest.
float opRound(float field, float r) {
return field - r;
}Box
sdBox(size)
Rounded Box
sdRoundedBox(size, radius)
Compensated Box
size = size - c(radius)
Uniforms
Shader Parameters
Adjust the Size and Radius to see how they affect the field result.
Annular
Ring-Shaped
We can "fold" all negative field values using abs. If all distance values are considered positive, and a radius parameter is subtracted, we find the field that desribes the shell of a shape.
In a simple sphere field, this operation would return a ring field.
In the double annular example we simple apply the ring function twice, with two different thickness values.
// Returns the annular field with thickness "r".
float opRing(float field, float r) {
return abs(field)-r;
}Ring
opRing(sdSphere())
Annular Star
opRing(sdStar())
Double Annular Rounded Box
opRing( opRing( sdRoundedBox() ) )
Uniforms
Shader Parameters
Shape properties and annular thickness.
Conclusion
With a bit of practise, these techniques can easily be applied to your projects, allowing you to leverage some massive benefits.
The best results come about when you combine multiple techniques - Build primitives, combine them with boolean operations, distort your domain to warp your results, and use fancy sampling to get your results.
This articles doesn't even touch on 3D distance fields, nor Raytracing/Raymarching, the current standard sampling technique for 3 dimensions. We haven't look at storing additional shape information in field dimensions (such a material, normal, or lighting values).
For further reading, I'd highly recommend Inigo Quillez, and The Art of Code